Home of Mr. 5

继续记录一些要用到的 prophet inequality 相关的结论。（对无相关了解者可读性低）

最近做的东西和先知不等式牵扯极多，不妨更个博客记录一下这个领域的经典结果。

如果你上一门本科阶段的计算理论课，你通常会学到“泵引理”这个证明一个语言非正则的手段。

但是，泵引理条件并非语言是正则语言的充要条件。你自然要好奇，有没有什么条件，既是充要的，又易于使用（来证明非正则性）？

最近对图论里的一些东西比较着迷，读到了下面这篇论文：

Finding Paths with Minimum Shared Edges

这篇论文提出了一个叫Minimum Shared Edges的问题，并说明了该问题的决策版本是NP-Complete的。

这段时间在看关于无政府代价的东西，绕不过去的一个话题就是“自私路由”（Selfish Routing）。（别担心，这篇文章和它毫无关系）

讲到自私路由自然会遇到很多“网络流图”，比如说下面这个：

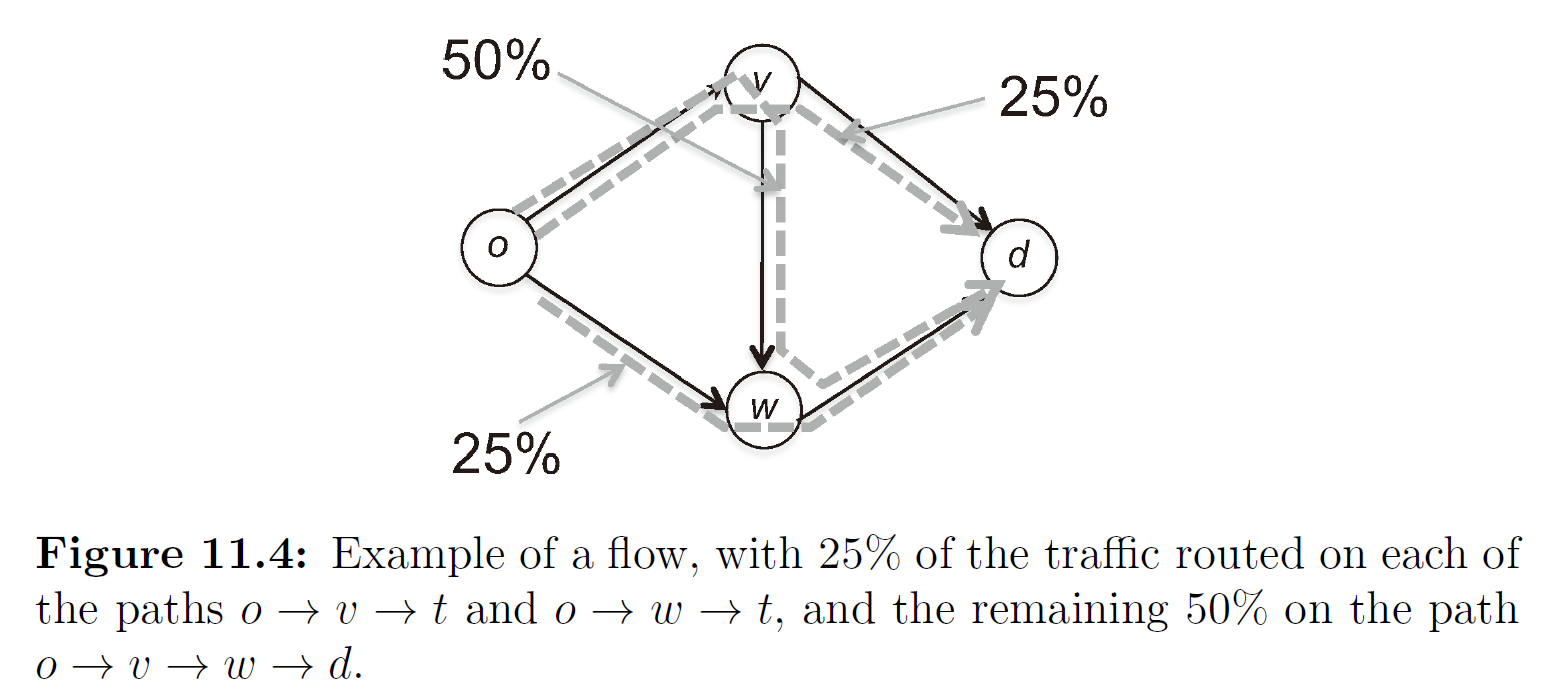
瞬时，我的奇奇怪怪脑筋又开动了。

这张图上总共有三条路径，总流量已知（比方说100），每条路径都有自己的流量，图中刚好都各自找到了一条仅属于本路径的边进行流量标注。我们把这种“能够给每条路径都找到一个无歧义的边进行标注”的情形称为“完全标注”。

有了这个有趣的概念，让我们一步步深入一些问题。

这其实是我开学的时候旁听了一节逼近计算的课的笔记（的拓展）。

由于研究关系，少量文章暂时被我移除了。研究完再放回来。

今天的计算理论课上，老师在讲NFA（非确定型有限自动机），然后就顺嘴提了一下以后要讲的NTM（非确定型图灵机）和DTM。他问：“NTM和DTM的计算能力一样吗？”（他指的是判定语言的能力）答案显然是一样的。他又问：“NTM和DTM的计算效率一样吗？”我脱口而出不一样，NTM更快。但又犹豫了。

老师说：“这个问题目前还不清楚，这就是P vs NP问题。”

I mean, hold on…

经过这段时间的学习，我已经对标题所述的这个科研点子有了比较系统的想法。