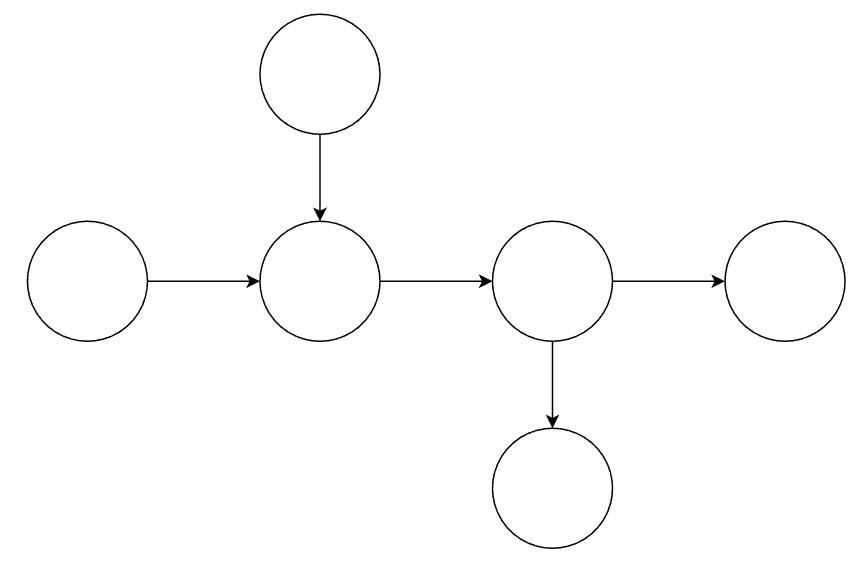
【科研点子】流量标注的可推断性与图兰问题

这段时间在看关于无政府代价的东西，绕不过去的一个话题就是“自私路由”（Selfish Routing）。（别担心，这篇文章和它毫无关系）

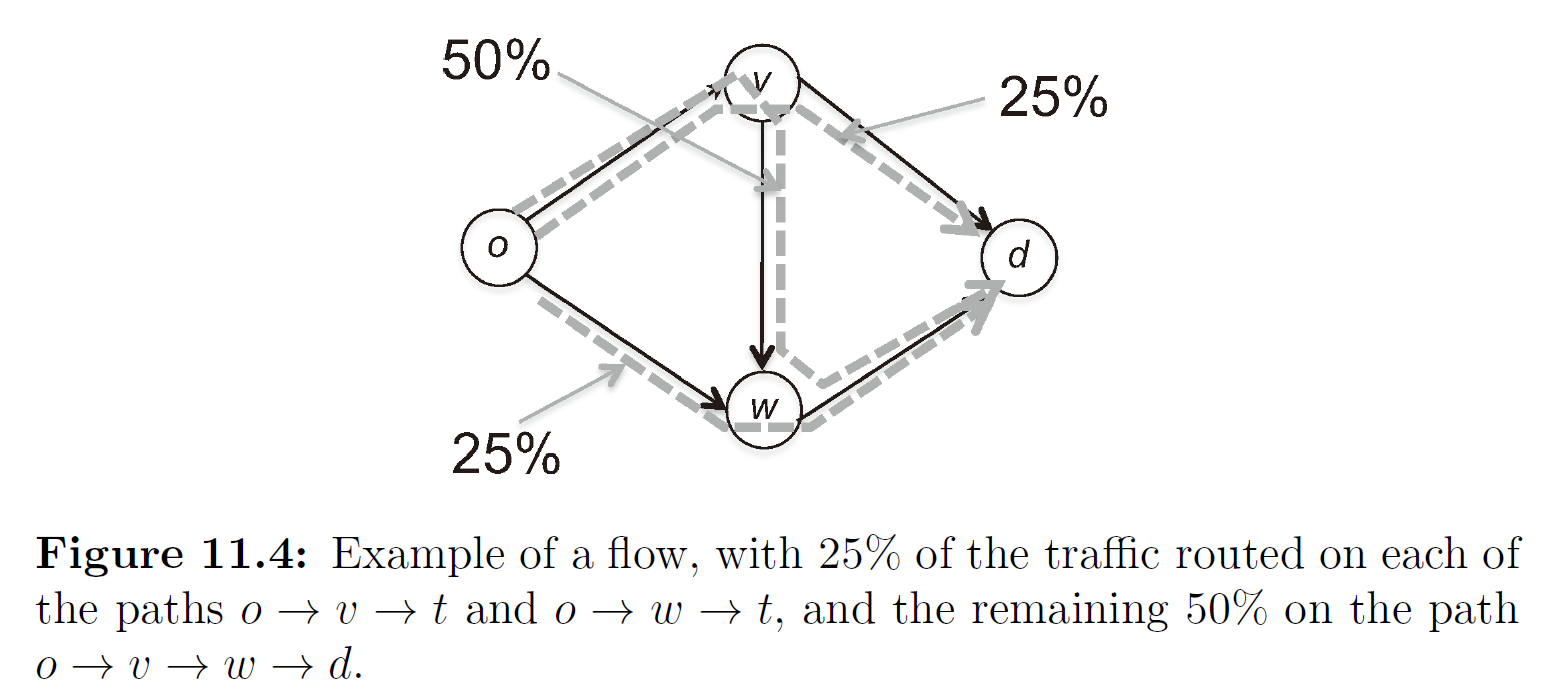
讲到自私路由自然会遇到很多“网络流图”，比如说下面这个：

瞬时，我的奇奇怪怪脑筋又开动了。

这张图上总共有三条路径，总流量已知（比方说100），每条路径都有自己的流量，图中刚好都各自找到了一条仅属于本路径的边进行流量标注。我们把这种“能够给每条路径都找到一个无歧义的边进行标注”的情形称为“完全标注”。

有了这个有趣的概念，让我们一步步深入一些问题。

所有图都可以进行完全标注吗？

第一个自然的问题就是：所有图都可以进行完全标注吗？

（注意，除非特别说明，这篇文章里提到的“图”都指的是“有向无环网络流图”）

答案是否定的。

很容易构造出这样的反例：

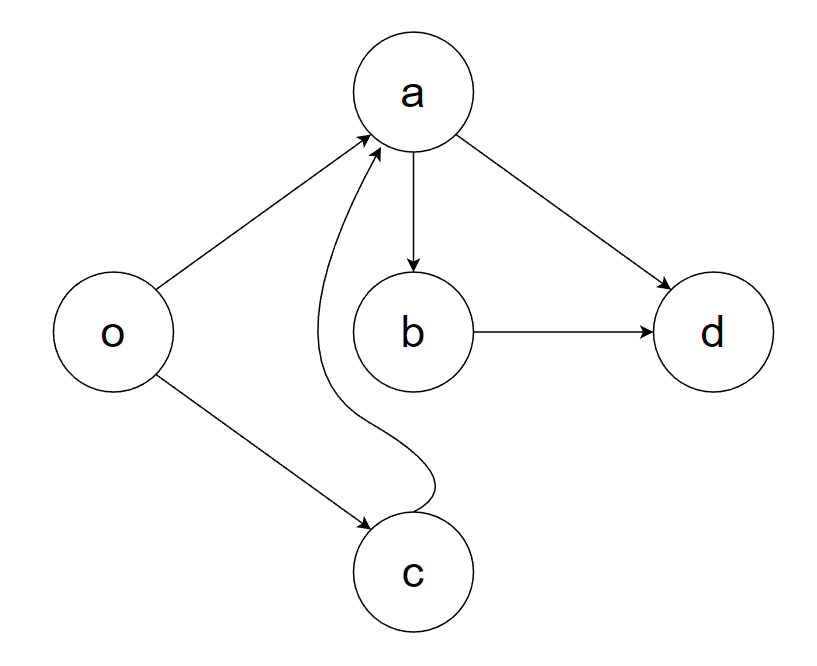
如果允许重边，那还可以更简洁：

事实上就是对前一张图进行了smooth out（平滑操作）。

这张图的任何一条路径都无法找到属于自己的独特的边进行流量标注。

所有图都可以进行完全推断吗？

我们在此处关心一个概念，那就是路径流量的推断。

比方说上面这张图，假如我现在仅标注A的流量，那么我们瞬间可以得到B的流量。这种行为就叫做“推断”，即根据已知的路径流量和总流量来推出未标注路径的流量。

这里说的完全推断指的是：根据现有的极大标注，推断出其他所有未标注路径的流量。

答案是否定的，这张图的就不行。它连一个标注都没有，自然啥流量都推断不出来。

存在部分标注图吗？

存在的，下面这张图就是部分标注图：

这张图的路径是可标注的，标注在处即可。

但是另外四条路径都不可标注。

因此这是一张部分标注图。

存在可以进行推断的部分标注图吗？

这是第一个非平凡的关键问题。

我们这里要求的甚至并不是完全推断，而是只要你能推断出一条不可标注路径的流量，那也算“可以进行推断”。

我们在这里给出一个猜想。

猜想1：

对于任意部分标注图，都不存在可被推断的路径流量。

当然，我们可以直接把这个命题推广到一个更一般但并不更难的断言，那就是：

对于任意极大标注图，都不存在可被推断的路径流量。

这是因为，极大标注图包含 完全标注图、部分标注图、不可标注图 三种情况，第一种和第三种都是立即成立，所以只剩第二种情况是非平凡的。

部分标注图的一般结构

要研究这个猜想，首要的抓手就是部分标注图究竟是什么样的图，或者说部分标注图里包含什么样的结构使它称为了部分标注图。

我们在刚才的讨论中多次用到了一个最简的不可标注图的例子，我们暂且将其称为“结构X”：

一个合理的猜想是，所有的部分标注图中都含有结构X或结构X的某种变体。

经过研究，发现事实确实如此。

在给出这一定理之前，我们首先将前述的各类对象进行形式化定义。

考虑任意有向无环网络流图，上的全体路径的集合记为。

对于任意，如果存在使得，则称是可标注的，并将称为的一个可标注边或特殊边；否则称是不可标注的。

（我们不严格地用表示边在中，用表示顶点在中，我们还将使用“边在点右侧”这样的说法表示沿行走时首先到达，并在后续才通过）

可标注路径集记为，不可标注路径集记为。

我们关注的上的流量是“路径相关”的，而不是通常的“边相关”的。

一个网络流图的路径流量在定义上是非常放松的（相对于边流量）：

（非负）

，其中为总流量。（正则）

则就是一组合法路径流量。

严格起见，我们在后面的定理中还要用到一个平凡的条件，那就是半标注图的可标注路径的流量和小于。（否则可以立刻推断出剩下的未标注路径流量都为）

另外，我们还需要知道smooth操作的含义：

我们把进行smooth之后产生的新图称为

若满足，则为完全标注图；

若满足，则为不可标注图；

若既不是完全标注图也不是不可标注图，则为半标注图。

上的路径流量推断问题指的是下面这个问题：

给定，已知，

求。

在我们的情境中，有多解和无解都统称为不可解。

现在我们终于可以陈述第一个定理。

定理1：

是半标注图

具有下面两种子图中的至少一种

1. 

2. 

要证明这一定理，只需要注意到下面的引理：

引理1：

对于任意，若存在，使得，则上在右侧的边都不可标注。

引理2：

对于任意，若存在，使得，则上在左侧的边都不可标注。

对应的，

引理3：

对于任意，存在顶点对， 且 在左侧，使得。

上述引理的正确性都是显然的。

引理1和引理2给出了定理1中的，引理3给出了。

我们便可以得出完整的定理1。

由定理1立刻可以得到下述推论：

推论1：

若是半标注图，。

猜想1的证明

好了，现在我们知道半标注图的一般结构了。那么，怎么能够说明具有这个结构就一定无法推断呢？

事实上，从路径流量的定义可以看出，我们至多能在不可标注路径只有一条时将其推断出来。

而推论1告诉我们，半标注图至少有4个不可标注路径。

因此，猜想1得证。

一些碎碎念

我一开始很快搞出了定理1和推论1，但是却一直没想起来去搞路径流量的定义。导致我居然一开始不知道最后一步怎么证明猜想1。其实定义之后猜想1就特别显然了。

看起来挺弱智的，不过就像丘成桐说的：“世界上没有白费的学问”，这些简单的工作可以引导我们进一步思考更深入、更正确的问题。

图兰问题

接下来我们思考，定理1中提到的两种基本结构在随机图中常见吗？有多常见？

这是同样是一个比较模糊的问题，我们一步步做下去。

首先，设图的顶点数为，如果不允许出现这两种结构，那么最多可以有多少条边？

这类“不允许出现某种子图的图最多有多少边”的问题叫做图兰问题。如果我们把目光focus在第一种结构（在图论中称为），那么这个问题已经在近几年得到了学界解答。

令，就得到

而如果加上第二种结构，并考虑它们都是在smooth意义下的，最终的图兰数显然应当介于和之间。即

定理2：

若图的，则的。

让我们忽略掉这种常数的区别，只要知道是级别的就好。

对于随机图，图的边数遵循二项分布。则随着增大，的图的边数都约为，是的。那么我们可以立刻得到——

定理3：

在随机图意义下，当，完全标注图占所有图的。

（这里有一个我不太能直观到的问题，就是半标注和不可标注图各自的占比是多少）

我们把边数为（或接近）的图称为“典范图”（类似信息论里的典范序列）。一个自然的问题是，在典范图中，的密度或数量是多少？

注意到，图的顶点数为时，条边一定会产生一个。那么，在总共条边里任选个，每次都会有一个，这意味着图中至少有几个呢？这就是一个简单的鸽巢问题。显然应当也有个。（注意，尽管结果是正确的，但这一段证明极不严格，此处鸽巢原理的应用需要依赖一些前提，比如仅含有常数条边，因此我们认为一个可以与常数个边对应起来）

那么不可标注路径有多少呢？我们知道了的数量，那么就可以利用这个数量来估算路径数。但是如果一些之间并不联通，那么就会导致一些被浪费，在计数时难以考虑。幸运的是，我们有

引理4：

联通图占所有图的。

这个引理很容易证明，可以参见reference request - Asymptotic number of connected simple graphs of n labelled vertices - Mathematics Stack Exchange

又由于典范图占所有图的，可知连通典范图占所有图的。

好的，现在不用担心不连通的情况了。

为了估计下界，我们假设所有都排成一列（中心可列在同一条路径上），此时是利用率最低的。

那么有——

定理4：

也即

更进一步的猜想

我们猜测，不仅未标注路径的流量是无法推断的，就连这些路径上的任何一条边的流量也是无法推断的。

可能的实际应用？

化学物品等类似流水线上的混合与分拣。

更多碎碎念

还有一些细节问题没有处理：

我们对路径流量的定义显然是没有问题的，但是要在代数上说明这个定义和传统的对边流量的定义是相容的，还需要更严格的证明处理。

（编写中）