【理论学习】信息论
文献:A visual introduction to information theory
什么是信息?
信息,是不确定性的反面、是随机性的反面。能够消除我们对随机事件的不确定性的东西就是信息。
什么是bit?
非信息论情形里,bit是一个为0或为1的一位数字。
信息论中,bit既是信息熵的单位、也是信息量的单位。
一个有
对于一个随机变量,每当我们能排除一半的随机性,我们就获得
比如: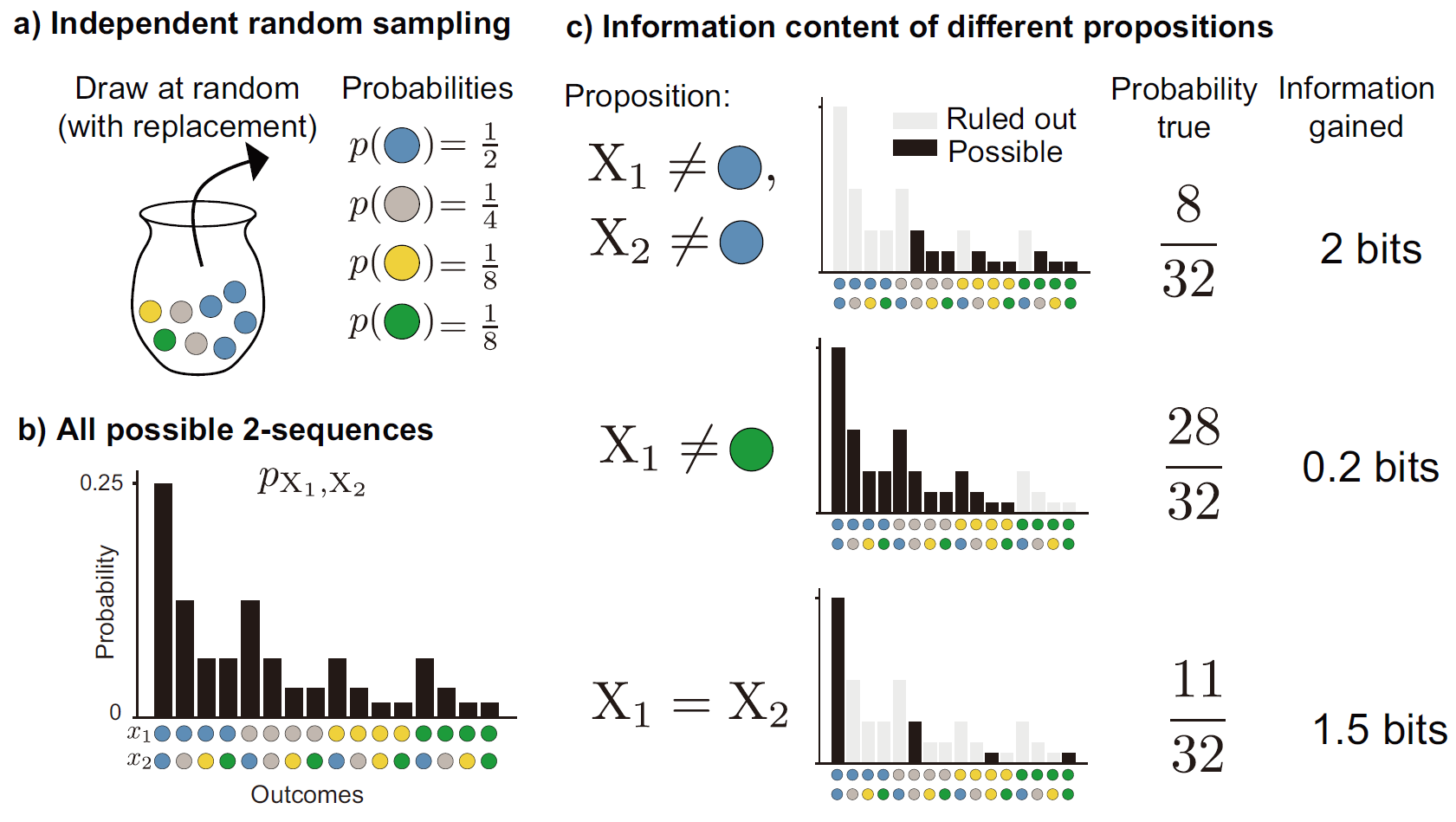
在已知
公式:
什么是信息熵?
一个随机事件的概率加权平均信息量就是信息熵。
公式:
信息熵也是平均来讲一个随机事件有多么出人意料的度量。
从这个角度讲,(在随机事件内的结果数
数据压缩
信息熵也是一个随机事件序列的最短编码的平均长度。
比如:
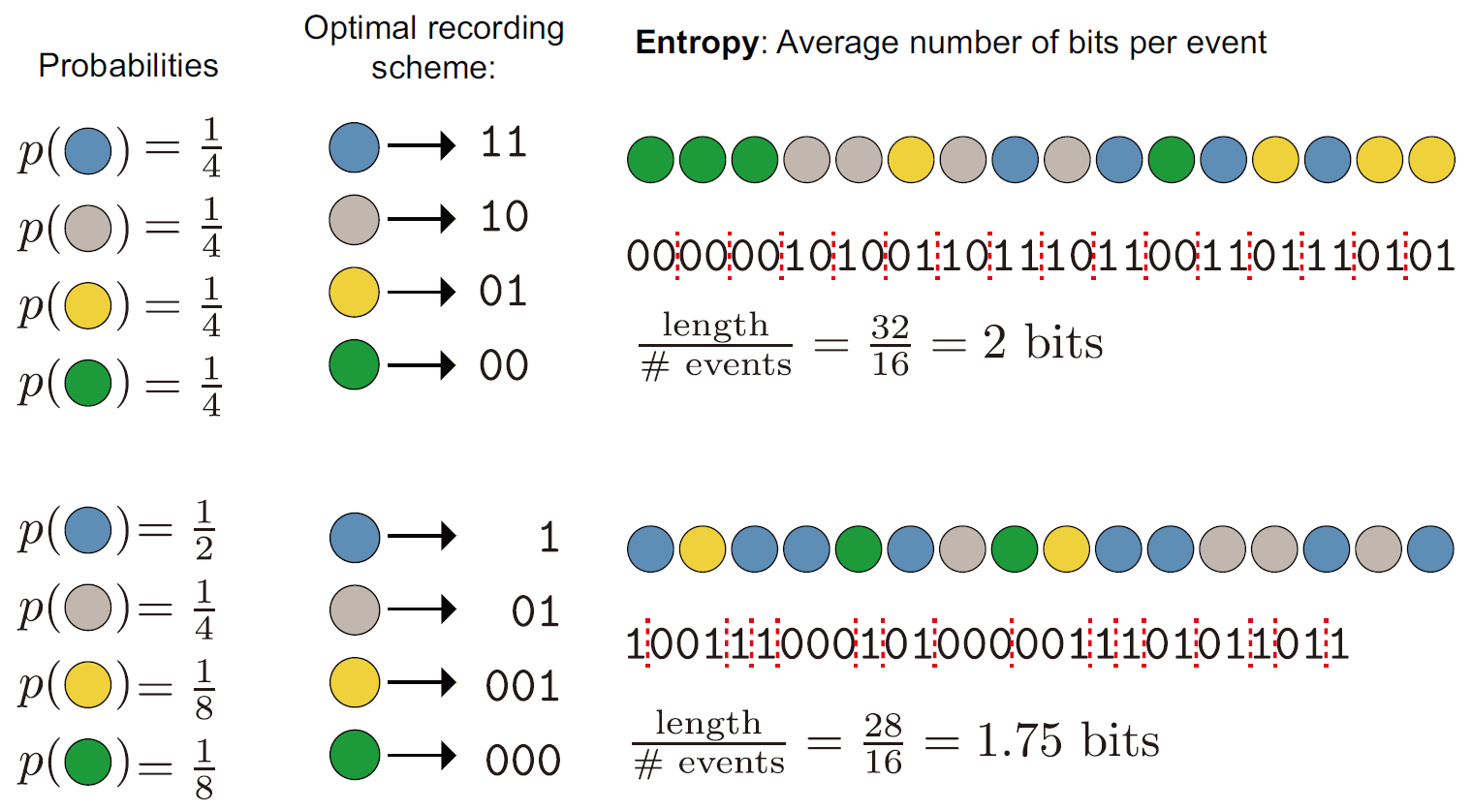
每一个颜色都按照自己的信息量(bit数)进行编码,这就是概率平均意义上最短的编码方案。
怎么方便地找到这个最短编码呢?(比方说很多时候bit数不是整数该怎么编码?)
其实就是哈夫曼编码。
信息熵与平均编码长度之间的对应也更进一步地直观展现了“信息熵是概率加权平均信息量”的观点——正因为平均信息量变大了,所以需要更长的符号来编码。
剩余度
一个随机事件的剩余度是它的实际熵与其通过调整结果概率所能达到的最大熵之间的差。
最大熵就是所有结果的概率相等时达到:
其中
则事件
一般数据压缩的界限
在讲信息压缩的时候,我们提到了两个例子,但是这两个例子都是为了更好地展示熵的概念精心设置的,它们包含了两个不够一般化的假设:
所有结果的概率都形如
,这样我们得出的各个结果的熵——也就是各个编码的长度才是整数。然而大部分情况下,我们是得不到整数熵的。因此,随机事件结果的熵之和永远小于等于其各结果的编码长度之和(除以一下 也就是事件熵永远小于等于平均编码长度)。为了让实际编码长度逼近理论界限,我们可以使用块编码策略,也就是对“某几个结果依次发生”的结果序列来进行编码。当编码的序列长度越来越长时,平均编码长度也越来越靠近事件熵。 作为示例的两个序列里的各个结果的出现次数都刚好符合它们的数学期望。我们把这样的序列称为典型序列。
典型序列 与 渐进等分性
对于一个结果(or 一串结果),如果其包含的信息量接近其从属的随机事件的熵,那么这个结果就是一个典型序列。典型集是全体典型序列的集合。
对于由
对于一个小正数
我们要问:
我们有如下事实打消这种顾虑:无论正数
因此,根据这个不等式可以推知,当
这被称为渐进等分性。
关于渐进等分性更好的介绍参见这篇文章。
一般数据压缩
既然典型序列构成
而且由于渐进等分性,这样的编码也是几乎无损的。因为未被编码的那些非典型序列并不占有概率质量。
有趣的是,这种几乎无损的编码会舍弃掉出现可能性最大的序列!
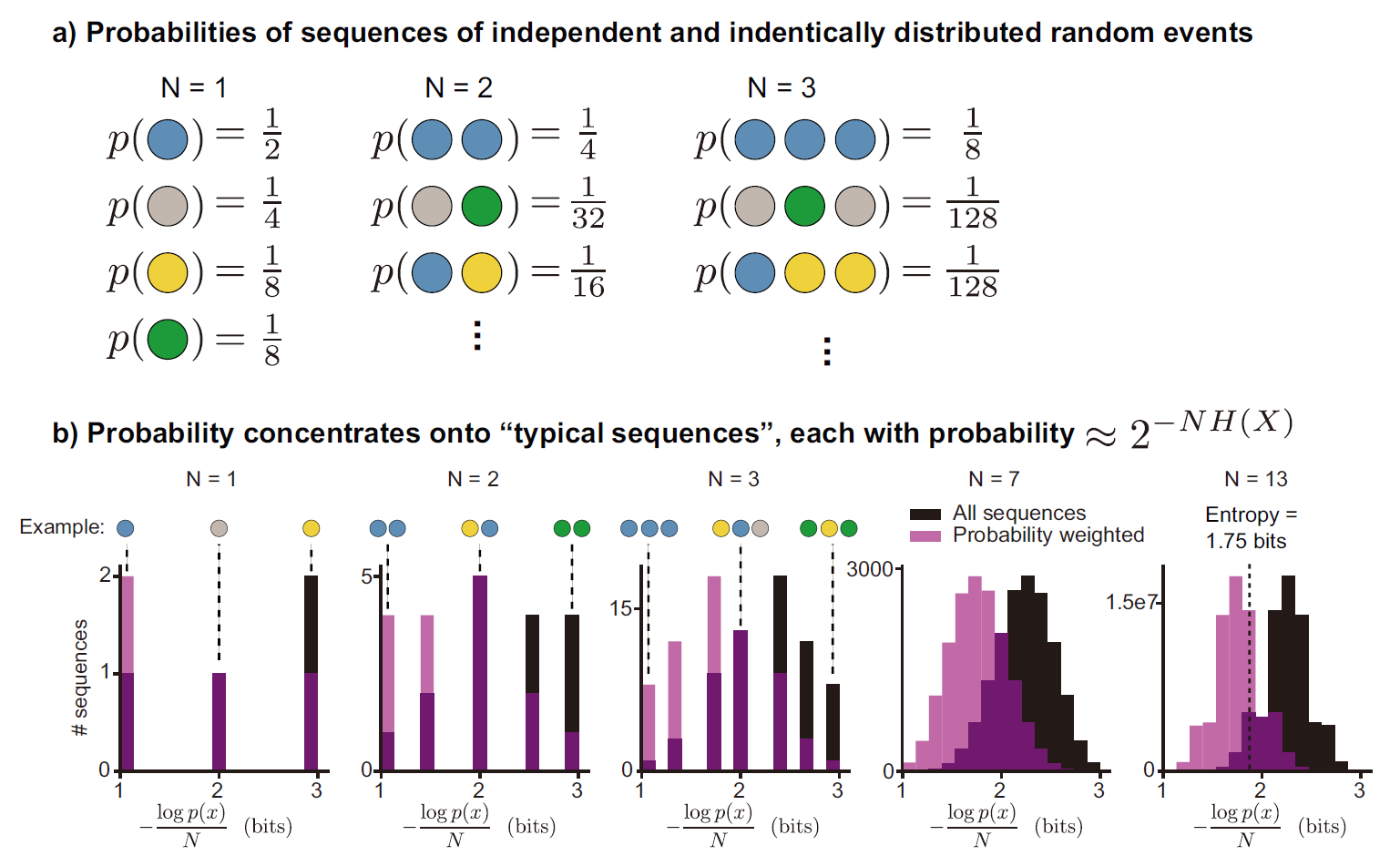
上图中,全部为蓝色的序列无论在
(横坐标是序列的平均熵,浅紫色是该平均熵下序列的总概率质量,黑色是该平均熵下有多少种序列,深紫色只是浅紫色和黑色相交的地方)
互信息
刚才举的例子里都是不同颜色的小球,形状都是一样的。现在我们假设颜色
互信息,就是当你知道这两个随机变量的其中一者的结果时,能够多大程度上增进你对另一个变量结果的信息。
互信息记作
它有几个基本性质:
(因此顺序并不重要) (两个变量独立的时候就会是 ) ,这是在说 揭露 并不会导致比自己所在的随机事件的信息量还要多的信息,也不会导致比 所在的整个随机事件的信息量还要多的信息。
衡量两个变量之间的依赖关系的另一种常见概念是“相关性”(协方差)。互信息可以理解为相关性的推广,因为我们常用的相关性通常衡量的只是线性相关性,而互信息可以表示任何变量间的统计依赖性。
为了计算互信息,我们首先要对联合分布上的信息有所了解。对于联合分布上的任意一个点,我们有它的点间互信息:
它表征的是这一特定结果下
上面这个式子也等价于
以及
第一个有容斥原理的意思,
第二个更清楚一些,它将两个事件同时发生的概率与事件独立时同时发生的概率进行比较。
这个式子同时也等价于
它可以被解释为
要注意的是,点间互信息可以取负值,且无界,这使得这个概念的理解和使用有一定的困难。也因此,学界提出了许多点间互信息的变体,比如“正值点间互信息”“标准化点间互信息”等。
现在我们可以定义互信息,它就是概率加权平均的点间互信息:
类似信息量,互信息也是每消除一半的随机性就增加
比方说
当然,如果颜色有等概率的
条件熵与联合熵
条件熵,顾名思义,就是在一定结果发生的前提下事件的熵。要定义条件熵,首先要定义一个特定结果下的点间条件熵。
点间条件熵就是在给定其中一个变量结果的前提下,另一个变量的熵:
条件熵就是点间条件熵的概率加权平均:
也即
如果我们观察到
联合熵的定义很简单,就是把“熵”推广到了多变量事件上:
注意到,当
上述概念的联系
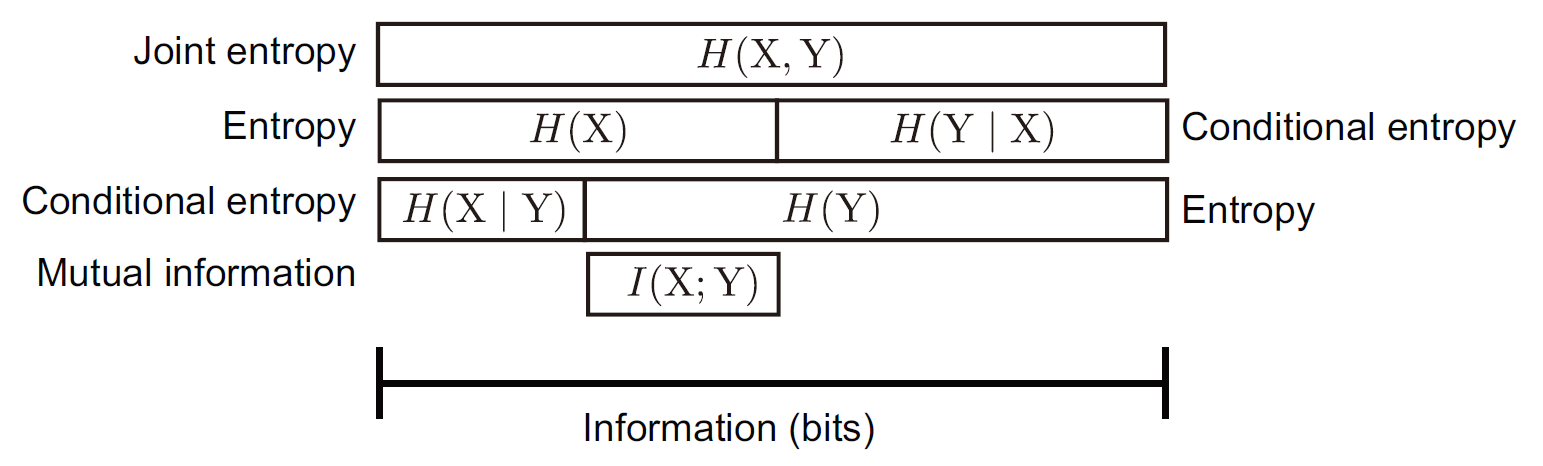
随机过程的熵率
在上面的所有例子里,事件的多次发生都是独立同分布的。比方说在编码的例子,拿出彩色小球每次都是独立同分布的,这一次拿出的小球的颜色并不会影响下一次的颜色的发生概率。对于一般的,也就是不一定独立同分布的情形,这种连续的事件发生过程我们通常称为随机过程。记为
在独立同分布的情形下,我们有概率密度or质量函数
此时,
一般的,熵率定义为:
我喜欢叫它平均熵率,类似于物理里的“平均速度”。
让我们考虑这样一个魔法罐子,每次抽出某个颜色的球,就会增加下一次抽到该颜色的概率为

另外一种熵率的定义是用的条件熵:
我喜欢叫它瞬时熵率,类似于物理中的瞬时速度。
两种定义下的熵率随着轮数的变化曲线已经在图d中给出。可以看出“平均速度”最终和“瞬时速度”逐渐重合。
在上面的模型里,每轮的概率分布只取决于上一轮的结果,我们把这样的随机过程称为马尔科夫链,它的瞬时熵率显然可以简化为:
无论采用哪种定义,上述模型的熵率随着
其中
其实也就是概率分布有平移不变性。
当然,我们所说的“平稳”通常指的是渐进平稳。比方说上面的模型里
随机过程的剩余度
把剩余度的概念推广到随机过程上:
显然当每次事件是独立同分布且各结果概率均等时有
概率密度与微分熵
把熵的概念推广到实轴上的概率密度函数上:
但是这个推广有不少问题。首先,它不再具有离散情形中“表示变量的所有结果的bit数的平均值”,因为要表示连续情形事实上需要无穷长的bit数。其次,它可以是负值,这和离散情形也不同。还有批评指出,这个公式对作为量纲量的概率密度函数(单位为
一个解决办法是把实轴分割为无穷个宽度为
不过,互信息的定义并没有受到上述问题的影响:
(可以注意到
率失真理论
我们之前提到过,有的时候,我们可以容忍一定程度上的信息失真、损失,以达到更简短、更高效的信息传输或信息压缩。那么我们自然要问像这样的问题:失真程度和编码简化程度的关系是什么?和保留的信息量的关系是什么?
率失真理论回答的就是这些问题。
首先,我们需要一个失真函数来衡量失真程度:
$$
(编写中)