【论文评述】Online Matching and Ad Allocation

文献：Mehta, A., 2013. Online matching and ad allocation. Foundations and Trends® in Theoretical Computer Science, 8(4), pp.265-368.

本文将不断更新

---

第一章

Theorem 1.2 证明：最大匹配中的任何一个边添加到极大匹配中都无法再扩展极大匹配（极大的定义），因此最大匹配中的每条边都至少含有极大匹配中的一个点，又因为最大匹配的每条边都有两个点，所以极大匹配规模至少是最大匹配规模的一半。

Tip1：类复杂度的诞生就是来源于Blossom algorithm。

Tip2：Finding the number of perfect matchings in a graph和Calculate the Permanent of a matrix是等价的，并且因为这个问题诞生了类复杂度。

---

第二章

常用问题模型

1. Online bipartite matching

   最经典的模型，尝试寻找图的最大匹配。

2. Online vertex-weighted bipartite matching

   点有权重，尝试寻找总权重最大的匹配。

   将点权都设为一样的值那就等价于模型1。

3. Adwords

   每个点都有一个预算，每条边都有一个价格。连边就相当于按照价格花掉一些预算。目的是让总开销最大。重要子问题——The small bids assumption:相比预算，每个价格都很小。

   预算都为1且价格都为1则等价于模型1。

   预算等于点权 且 价格等于（与其相连的点的）点权则等价于模型2。

4. Display Ads

   每个点都有一个容量，代表能连几条边（因此是整数）。每条边都有一个边权（实数），目的是让总边权最大。

   重要子问题——The large capacity assumption：每个点的容量都很大。

   有时我们会讨论带有free-disposal性质的display ads问题，也就是可以移除已匹配的边来选择更好的边。

   容量和边权都为1则为模型1。

   容量为1，边权为关联点的点权则为模型2。

   模型4与模型5不可通约。

   （注意，以上说的“点”“每个点”都是指二部图中的某单个部中的点）

5. Online Submodular Welfare Maximization（SWM）

   这是前面所有模型的超集。

   左部每个点都有一个非负单调的次模函数，函数的定义域是右部点的幂集，值域是正实数集。一个左部点与哪些右部点相连，那这些右部点构成的集合就是自变量的值。

   模型5通约到前四个模型的方式如下：

   

6. Generalized assignment problem (GAP)

   是模型1~4的超集，左部点有预算，边既有开销又有权重，目标是总权重最大化。

   不再详述如何归约。

部分模型的关系图如下: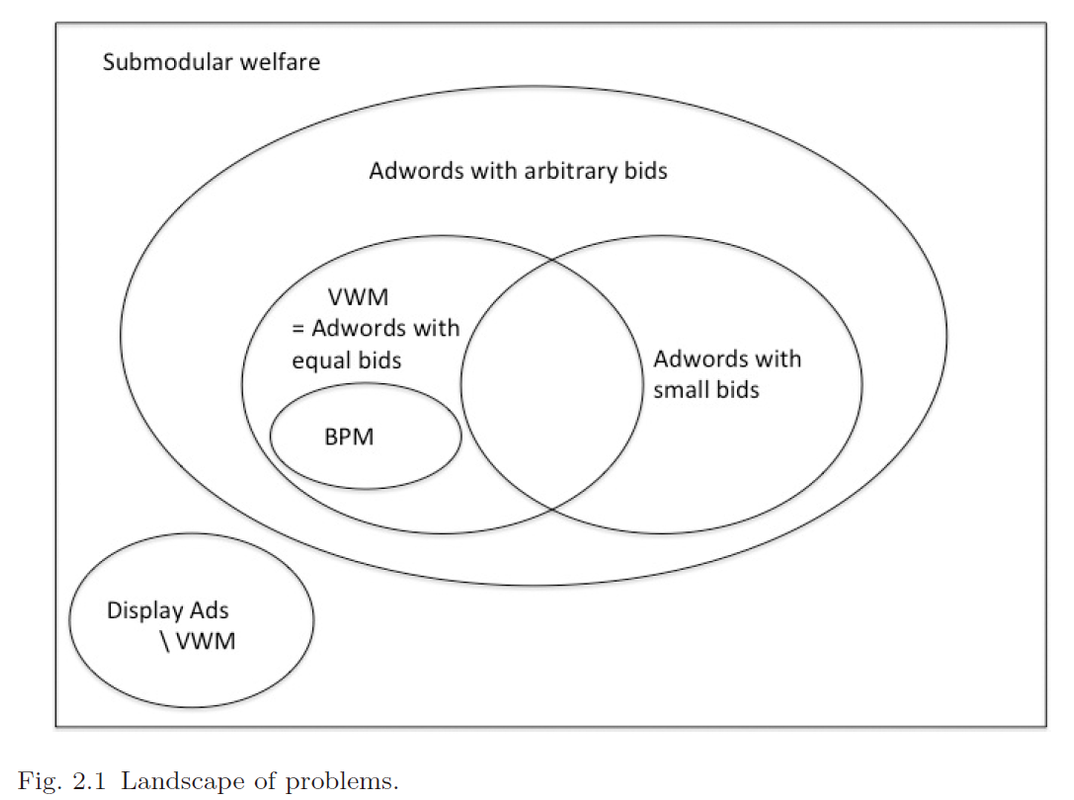

常用输入模型

1. Adversarial order
   “最严苛”的一种模型，有一个对手提前知道你的算法的内容，并能够决定构造什么图给你，且能决定右部点的到达顺序。

2. Random order
   图的构造仍然是adversarial的，但这次对手无法决定点的到达顺序，而是随机到达。

3. Unknown IID
   定义点类型，即对相邻点、权重等等与右部点相关的性质的一种类型编码。有T种点类型，有一个T上的分布D，每次根据D随机选择一个类型，作为一个右部点实例化。D对算法来讲是事先未知的。

4. Known IID
   D事先已知。

Competitive Ratio

简单来讲，，G是所有可能输入，对于随机算法，就是，当然有的时候可能是max，取决于你在度量什么，想要将其最大化（比如衡量匹配的规模）就要用min，想最小化（比如时间）就用max。

关于这些输入模型的competitive ratio（后面常常简称为C.R.），有一个基本的不等式：

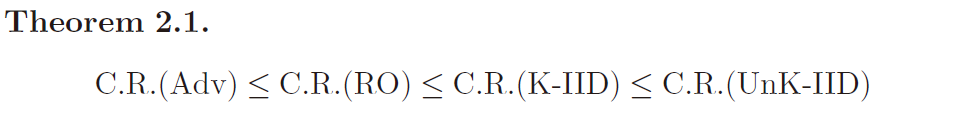
一开始我还觉得奇怪，怎么K-IID的表现不如UnK-IID的表现呢？其实你想，你known了，人家最佳也known，那么对于一个特定的ALG，K和UnK是没有区别的，因为它是特定的K。但是对于位于分母上的最佳算法OPT，它一定能表现得更好。
你可以说K了一定比UnK能设计出更好的算法，这没错，但competitive ratio是一个比例！以OPT为分母的比例！

因此，通常（特别是在这篇文章）我们说某模型or某问题更加“困难”，它不是指会让算法必须跑更长时间，而是在C.R.意义下更难取高。

关于各个模型下各类问题所取得的最佳成果：

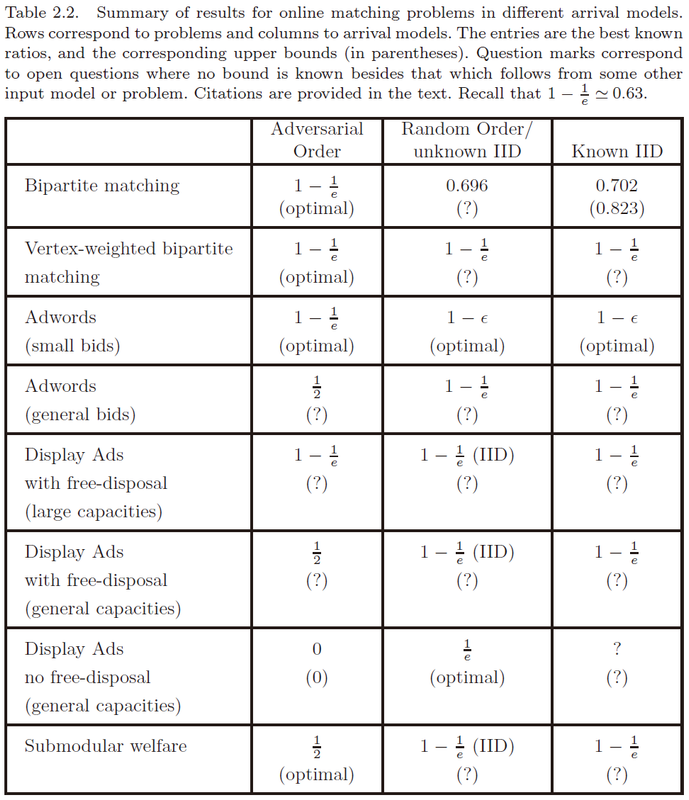
如果我没理解错自己老师的成果的话，Adwords在general bids下的competitive ratio已由张乾坤、张宇昊和黄志毅提升到0.5016——AdWords in a Panorama。

Offline

上述问题在Offline下的整数规划模型：

除了Adwords，其他三个问题都已经有多项式时间的解决方案。

带small bids约束的Adwords在的近似率下也有多项式解决方案，其中为图的。

另外，没有small bids约束的Adwords在要求近似率超过的情况下是的，目前最好只能做到。达到前学术界经历了（由Garg等人取得）、（由Andelman和Mansour取得，在所有budgets相等的情况下还能提升到）的过程，以及（由Azar等人取得），的结果事实上证明了offline版本严格简单于online版本（因为已知已经是online的一些特殊情形的上界，一般情形只会更难）。

GAP是上面四类问题的超集，它的整数规划模型如下：

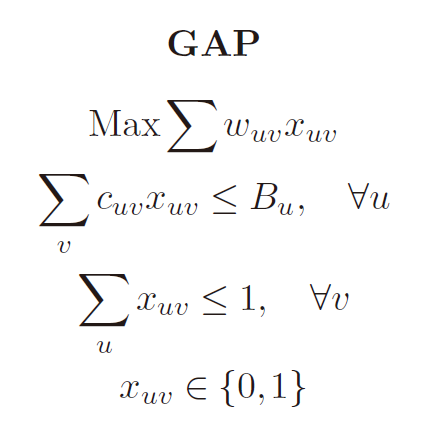
目前GAP最好的近似率应该是，由Chakrabarty和Goel取得。

至于Submodular Welfare Maximization问题，它被证明在近似率好于的情况下是的。

这里提一个SWM的子问题，或者说特殊模型：value oracle model。它是指在你需要获得某个集合对应的次模函数的值时，你是从一个谕示（相当于黑箱）里直接获得。

在该模型下，Vondrak取得了的近似率。Mirrokni等人证明了，在该模型下如果要打破的近似率，需要指数级的通讯量。

---

第三章

本章主要讨论Online Bipartite Matching。

Adversarial Order

最简单的想法就是贪心，只要有还能匹配的点，就无脑匹配。

对于确定性的贪心算法，下面这张图告诉我们它的 C.R. 一定不会超过。

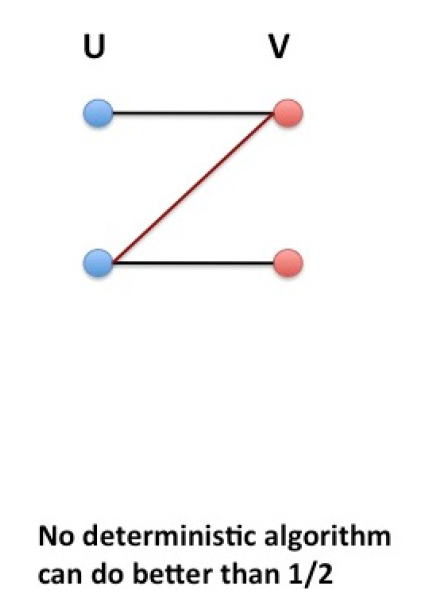
而第一章中的告诉我们，也是greedy的下界。

那么我们就有：

朴素的random算法（只要有点就随机匹配一个）在这张图上有更好的表现，匹配数期望为。而且可以知道的是，由于random算法本质上其实也是贪心的，所以它也一定能在所有输入上取得极大匹配，因此random一定有至少。但是朴素的random算法真的就比greedy在competitive ratio的意义上要强吗？还是同样也止步于呢？

下面这张图告诉我们random的C.R.同样为。图中粗粗的双向箭头表示V的上半部分的每个点都和U的下半部分的每个点有边。比方说，U和V都有n个点，那么V上半部分的任意一点都有条边，其中一条是图中的细边，条与U的下半部分相连。

直观上，random大概率会导致大量V上半部分的点与U下半部分的点相连，导致V下半部分到达后几乎已经没法连了。（当然可以严格证明）

我们有：

这个例子似乎昭示着一种困难的境遇，也就是说，为了超越，算法似乎必须天才般地知道哪条边是细边，这似乎不可能。

然而，由Karp等人提出的著名的Ranking算法达到了的C.R.，也是所有算法可能取得的最高C.R.。

Ranking算法先随机对U中的点进行排序，谁在排序中靠前谁的匹配优先级就更高。然后再开始接收输入并匹配。

首先谈谈对这个算法为何更好的直接感受。

感性地讲，朴素的Random还是太规律了，也就是它保证了每个可匹配的点被匹配的概率都相等，这其实仍是一个很强的性质，因此通过对V中每个点的可匹配点的关系的精心构造，该性质可以被利用，产生棘手的输入。但是Ranking舍弃了这一性质，“更随机”了。

注意，在考察Adversarial Order下的随机性算法的C.R.时，必须提前固定input order（当然，本质上确定性算法也相当于提前固定了input order，因为了解确定性算法的的code也就已经能预测确定性算法在任何输入中的每一步行为，没有必要在中途修改input order），这就杜绝了根据每次的匹配结果来猜rank的可能性。

那么具体怎么证这个C.R.呢？单单这个证明，已经可以称得上汗牛充栋，每过几年就要出来一个新证法。我的第一篇博客就是讲的最近的一个简单证法。

第三章用的是Birnbaum和Mathieu提出的证法。简单讲，就是考虑形如的二元组，其中为排列（即对U中点的一个排序），为U中的点。即在下被映射到的位置。现在fix一个输入，如果使得是被匹配了的，那就说这是一个Match event，否则就是一个Miss event。证明发现了：存在一种映射方法，使得任何一个Miss event都可以映射到n个Match event，且不同的Miss event不会映射出同一个Match event。

从而约束出Miss和Match的概率关系：

令，有

再用凸分析里包括一种叫Factor-Revealing LP在内的方法分析可得：

于是：

那么这个C.R.是不是紧的呢？是的！Karp等人在1990年已经证明了这一点。这里我们给出一个把Ranking逼到的实例：

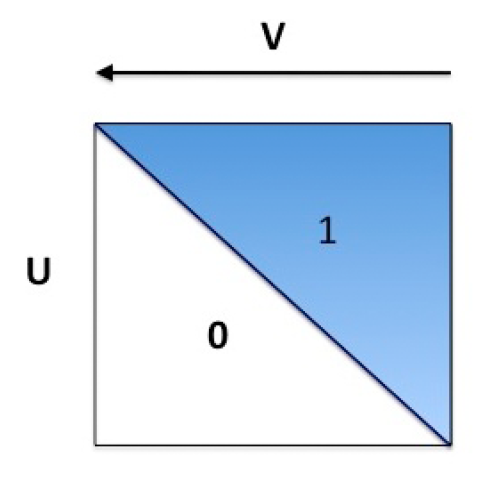
这是一个邻接表，箭头表示V揭示的顺序。很明显perfect match只有一个，即对角线。

Random Order

Random Order严格简单于Adversarial Order。

Greedy就可以取得的C.R.，分析证明和Adversarial下Ranking的C.R.证明几乎一模一样，因为V的顺序random本质上和U生成一个随机的优先级顺序是一样的。

同时，学界还得到了以下结果：

那么Ranking算法现在表现如何呢？学界目前有以下结果：

也就是说一个比较健壮的图可以让Ranking表现得明显更好。

目前这个领域主要有两个研究方向：

1. 将C.R.的上下界拉得更近。

2. 找到其他对健壮图反应明显更好的算法的例子。

Known IID

目前先简略介绍一些结果。

为了简便起见，我们就假设 ， 为均匀分布。

令，其中 为所有类型点的集合。

Suggested Matching 是 KIID 的基本算法，它的基本流程是这样的：

1. 找到 的最优匹配 ，这个部分是离线的。

2. 当到达时，令 为 的类型，

   如果是可用的，那么就将 连给 。

   否则continue。

该算法可以达到紧的 的C.R.。

当然，这个算法看上去有点太“苛刻”了，要求点必须跟最优匹配保持一样的连接。假如不巧连续遇到很多同类型点，那么该算法只能将第一个匹配（注意我们是在均匀分布下考虑问题，所以这是一个小概率事件）。

Two Suggested Matching等算法就是从这个思路改进。它首先找两个“大匹配”，然后哪个可用就用哪个。

目前的一个开放问题是，当 n>2 时，如何较准确地分析 N-Suggested Matching 的性能？

---

该survey的阅读笔记暂且更新至此。