【论文评述】An Economics-Based Analysis of RANKING for Online Bipartite Matching

发表于 更新于 分类于

文献

Eden, A., Feldman, M., Fiat, A. and Segal, K., 2021. An Economics-Based Analysis of RANKING for Online Bipartite Matching∗. In Symposium on Simplicity in Algorithms (SOSA) (pp. 107-110). Society for Industrial and Applied Mathematics.

问题背景

这篇论文仍然研究的是最经典的在线二部图匹配问题，也即1990年 研究的那个问题。

 

有一个二部图 ， 开始已知， 逐个揭示， 随着 的揭示而揭示。

现在，需要在每次有 及与其关联的边被揭示时在线地直接给出 的匹配对象。

目标是使最终的匹配最大化。

 

这个问题已经由Karp等人给出了著名RANKING algorithm，即首先给全体 中的点进行随机排序，排序靠前者将在后续的匹配中被优先匹配（如果可以匹配的话），这是一个非常简单但却有效的方法。

Karp等人证明了RANKING algorithm的

同时也证明了这是经典的在线二部图匹配问题的最高competitive ratio，但是当时给出的证明比较复杂。

后续有很多人对这个证明给出了简化，这篇文章提到的经济学视角也已经不是新鲜事物了，但这篇文章还省去了很多例如linear programming duality的技巧，非常的简单。

因此，这篇论文发表于 Symposium on Simplicity in Algorithms (SOSA)，这也我第一次知道这个以“简化”为主题的会议，感觉挺好玩：）

解决思路

为了方便起见，假设两部的规模都是 ，后续可以推广。

 

我们采用下面这个经济学视角：

把 看作买家的集合，把 看作商品的集合，把 看作买家对商品存在意愿（没有边就代表没有意愿）。方便起见，意愿要么是，要么是 。商品的价格则来自一个分布（后面会讲用哪个分布比较方便），这就对应着RANKING algorithm里的排序（价格越低越受顾客青睐，相当于排名靠前）。

注意到， 。

那么我们就是要最大化匹配M带来的social welfare的期望，即 。

 

对于边 ，我们有 ，则 。

这样，我们就把福利拆解为了效用和卖家收益，这是这篇文章的第一个重要步骤。

接下来只要证明

即可。

 

考虑。

代表缺少了 商品后的图所产生的匹配。

代表 中与 匹配的商品的价格。

 

接下来有两个最重要的observation：

1、如果 那么 就一定被售出。

这是因为，就算先前揭示的买家一个也没有买 ， 也一定会买走它，因为它便宜啊。

这个observation给出了 的下界！

（价格的分布已知，要得到 就只需要知道在何种情形下商品会被卖出，但是这是一个很难度量的东西，我们就需要找到一个一定会卖出的强条件，同时还要跟随机变量挂钩才能计算，于是就有了该observation）

2、

这是因为在原来多一个商品 的情况下 ， 及先前的顾客都多出至少一个选择（有边则多，无边则不多），而且每个顾客还是只能买一个商品，那么留给 的商品只会更好不会更差，那么util一定不会变小。

这个observation给出了 的下界！

则

即

再聊聊

这个证明里使用了一个分布，也就是在 中随机取一个值 ，然后把 作为商品的价格。

我的概率论知识非常贫乏，自然要问，如果换一个分布呢？

例如，最简单的，直接在 中取 ，那么计算可得

也就是说，得到的期望的下界仍然是一个随机变量，对这个随机变量再取下界方可得到一个常数competitive ritio，由我们先前已经知道的结果可知，这个ritio并不紧。

那么，我们可以尝试完成这篇paper没有主动解决的一个问题，怎么证明 是紧的？或者说这个紧的ratio是怎么算出来的？

在这里首先提出一个猜想，不均匀的随机数采样永远可以等价为一个均匀采样结合一个关于该随机变量的函数，我觉得这个猜想很对，会概率论的应该一下就能证明，但是我的概率论知识不够，所以很抱歉。

那么我们就只考虑 上采样的 ，以 为商品的价格，函数单调增（这个纯粹为了方便）且值仍在 。

则我们要求

不是很会求这个东西，但可以知道 是它的一个解。

更新(2023/4/2)

关于那个概率的小猜想，证明如下：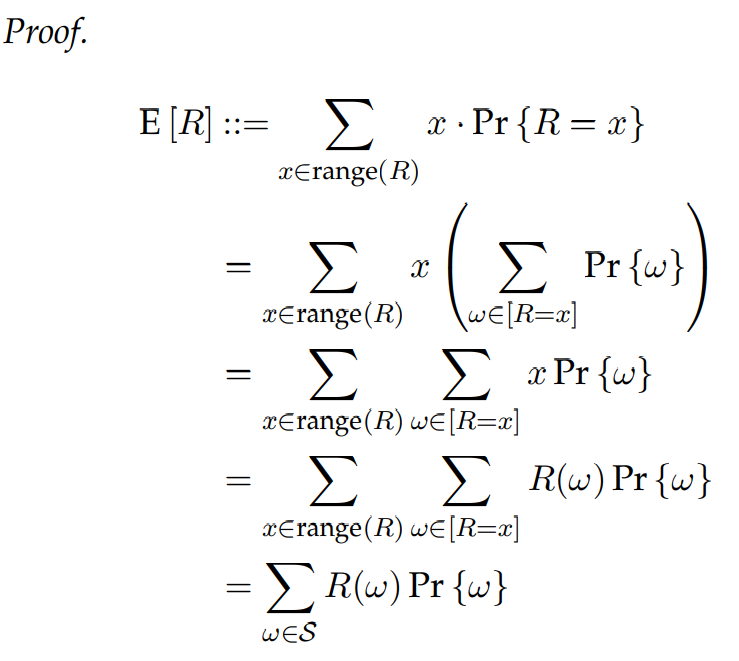

摘自该讲义

关于最后那个变分式，已经在2013年被人研究过了！
Randomized Primal-Dual Analysis of RANKING for Online Bipartite Matching
用Yao’s principle先估计出上界，然后猜出使得这个上界成立的函数。